(The Journal of the Society for Art and Science, Volume 20, No. 1)

View-dependent Projection Mapping Enhanced by Real Background

---- Additional Experimental Results and Videos (High Quality) ----

Khuslen Battulga (Iwate University)
Tadahiro Fujimoto (Iwate University)


The following are experimental results, some of wihch are shown in the paper and others of which are not. They are supplemented with videos.

E-1. Experiment in virtual environment

We firstly made experiments to simulate our projection mapping in a virtual environment constructed by OpenGL and evaluate the fundamental performance of our method. The virtual environment is shown in Figure E-1-0, which is almost the same as Figure 4 in the paper; Figure E-1-0 (e) is Figure 4 (c), and Figure E-1-0 (c) and (d) are not in Figure 4. The Values used in this virtual environment are shown in Table E-1-0. The detail of this virtual environment is described in Section 4.1 in the paper. Among the following five experiments, Experiment 1-5 is described in the paper, and Experiments 1-1 to 1-4 are not. In these experiments, a cube was used as a real object, an orange teapot was used as a virtual object, and colored boxes were used as objects in a real background.

[click]
Figure E-1-0. Virtual environment.

Table E-1-0. Values for experiment in virtual environment.
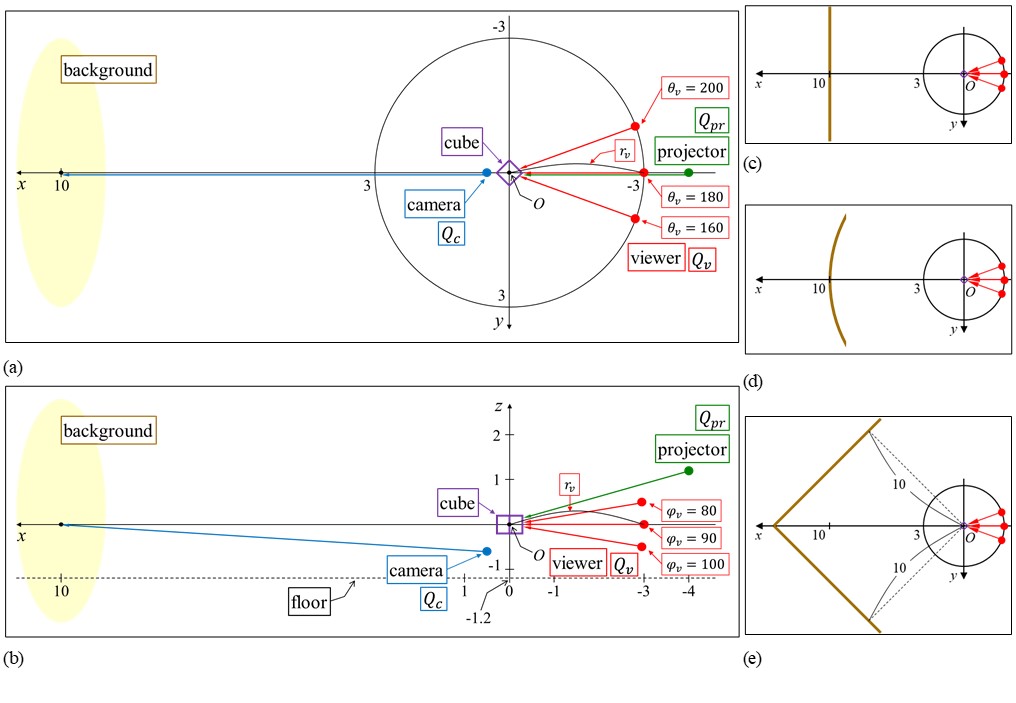
Position
[r, θ, φ]
(r: meters)
(θ, φ: degrees) 		Position
[x, y, z]
(meters) 		Gaze point
[x, y, z]
(meters) 		Angles of view
[αx, αy]
(degrees) 		Numbers of pixels
[Mx, My]
Viewer: Qvini 3.0, 180.0, 90.0 -3.0, 0.0, 0.0 0.0, 0.0, 0.0 20.0, 15.0 640, 480
Projector: Qpr 4.2, 180.0, 74.0 -4.0, 0.0, 1.2 0.0, 0.0, 0.0 38.0, 23.0 640, 400
Camera: Qc 0.8, 0.0, 140.0 0.5, 0.0, -0.6 10.0, 0.0, 0.0 57.0, 43.0 640, 480

Experiment 1-1: View-dependent projection mapping

The result of this experiment is shown in Figure E-1-1. This experiment shows the fundamental ability of our view-dependent projection mapping using the two-pass algorithm, that is, how the correct appearance of a virtual object is shown to a viewer moving around a real object. This experiment did not treat a real background. The images in Figure E-1-1 were obtained in the condition that the viewer saw the real object, that is, the cube from nine positions given by θv = 160, 180, 200 and φv = 80, 90, 100 at a constant distance of rv = rvini = 3.0 from the cube. The images in (a) are rendered images, that is, correct views seen from the respective positions. The images in (b) and (c) are projection images obtained for the projector's position Qpr by the two-pass algorithm. While the images in (b) were obtained by the original angles of view of the projector, the images in (c) were obtained by halving the angles in order to magnify the area of the teapot and show the detail of the "correctly distorted" projection image. The images in (d) are simulated real views seen from the viewer; the images were obtained by simulating the projection of the projection images in (b) onto the cube's surface. The comparison between the images in (a) and (d) shows that the correct appearances of the teapot were shown according to the viewer's positions.

A video of this experiment is shown in Video E-1-1.

[click]
Figure E-1-1. View-dependent projection of a virtual object for different viewer's positions in Experiment 1-1. rv = rvini = 3.0. (a) Rendered image. (d) Simulated real view. (b) Projection image. (c) Magnified projection image.

[click]
Video E-1-1. View-dependent projection of a virtual object for different viewer's positions in Experiment 1-1. rv = rvini = 3.0. Upper left: Rendered image. Upper right: Simulated real view. Lower left: Projection image. Lower right: Magnified projection image.

Experiment 1-2: Adjustment of projected real background

The result of this experiment is shown in Figure E-1-2. This experiment shows how a viewer background image is adjusted by background parameters LP, ΔθP, and ΔφP. The colored boxes, which simulated objects in a real background, were arranged close to the vertical plane which was parallel to the yz plane and 10 meters away from the origin O in the x direction; the plane is represented by the brown line in Figure E-1-0 (c). The boxes were rotated randomly; their centers were arranged regularly with random displacements within ±10 % of the interval between neighboring boxes horizontally and vertically on the plane and within ±0.1 meter perpendicularly to the plane. The length of one side of each box was 0.55 meter. In Figure E-1-2, the image (a) is a camera background image captured from the camera's position Qc. We mean a real view directly seen from a viewer without image conversion and projection by "directly-observed" view. The image (b) is a directly-observed background view seen from the viewer's initial position Qvini with Rvini = [3.0, 180, 90]. The images in (c1), (d1), and (e1) are viewer background images for the viewer's position Qvini; the images were obtained from the image (a) by the background planes P defined by different sets of parameters LP = 5, 10, 15, ΔθP = -45, 0, +45, and ΔφP = -45, 0, +45. Each of the bottom-left and bottom-right images in (c1) has a black area at one top corner; this area is out of the range in which the image (a) was converted. We mean a real view containing a real object with projection and the directly-observed background behind it by "augmented" view. The images in (c2), (d2), and (e2) are augmented views seen from the viewer's position Qvini; in each image, a dark central area is the cube's surface onto which the viewer background image in (c1), (d1), or (e1) was projected from the projector's position Qpr by using the two-pass algorithm while the remaining area behind the cube is the directly-observed background in (b).

The images in Figure E-1-2 show the practical usefulness of the parameters LP, ΔθP, and ΔφP. The change of LP moves the plane P forward/backward in the viewer's viewing direction, which magnifies/demagnifies the viewer background image and adjusts the sizes of all the boxes uniformly. The change of ΔθP and ΔφP changes the incline of the plane P, which distorts the viewer background image and adjusts the sizes of the boxes relatively according to their positions. The main purpose of our method is to make a viewer feel a virtual object merging into the real world by making the viewer not feel the presence of a real object by the background projection. For this purpose, the most important evaluation to the background approximation by the plane P is to evaluate how seamlessly the projected background on the cube's surface matches the directly-observed background behind the cube along the boundary of the cube's contour. The central image in (d2), which was obtained by LP = 10, ΔθP = 0, and ΔφP = 0, has the best seamless match between the projected background and the directly-observed background along the boundary; in this case, the plane P is the same as the plane which the boxes are arranged close to. The result of this experiment shows that our method can adjust the "boundary match" between a projected background and a directly-observed background easily, intuitively, and efficiently. This ability is important to achieve the merge of a virtual object into the real world.

A video of this experiment is shown in Video E-1-2.

[click]
Figure E-1-2. Viewer background images and augmented views for different background parameters in Experiment 1-2. (a) Camera background image. (b) Directly-observed background view. (c1), (d1), (e1) Viewer background image. (c2), (d2), (e2) Augmented view. The parameter LP = 5 in (c1), (c2), LP = 10 in (d1), (d2), and LP = 15 in (e1), (e2).

[click]
Video E-1-2. Viewer background images and augmented views for different background parameters in Experiment 1-2. Upper: Viewer background image. Lower: Augmented view.

Experiment 1-3: Projection of virtual object and real background

The result of this experiment is shown in Figure E-1-3. This experiment shows how our method achieves the merge of a virtual object into the real world by the view-dependent projection of not only the virtual object but also the real background. The images in Figure E-1-3 are augmented views seen from twenty-five viewer's positions given by θv = 160, 170, 180, 190, 200 and φv = 80, 85, 90, 95, 100 at a constant distance rv = rvini = 3.0. Each image has a dark central area of the cube's surface with the projection of the teapot and the background and the remaining area of the directly-observed background. The projector at the position Qpr could not project a projection image on the bottom face of the cube, which made the bottom face black in each image of φv = 100. Conversely, the top face of the cube is bright in each image of φv = 80. Background boxes were arranged close to the surface of a sphere, which is represented by the brown curve in Figure E-1-0 (d). The sphere has its center at the origin O and a radius of 10 meters. The boxes were given the same random rotation and displacement as those of the boxes used in Experiment 1-2. Then, if the distance LP of the background plane P is the same as the sphere's radius and the plane's normal vector N is the same as its base normal vector N0, the resulting augmented view for every viewer's position has almost the best boundary match between the projected background on the cube's surface and the directly-observed background behind it. Thus, we selected LP = 10, ΔθP = 0, and ΔφP = 0. Each image in Figure E-1-3 shows the above result although there are some slight gaps between the projected background and the directly-observed background along the cube's contour. The gaps were caused by the difference of the shapes of the sphere and the plane P as well as the approximation of the 3D shapes of the boxes by the plane P.

The brown checkered plane in the images of Figure E-1-3 is the floor. The boundary match between the projected floor on the cube's surface and the directly-observed floor is not appropriate. In particular, they do not match at all in the area near the cube, as shown in the images for φv = 80. This was caused by the reason that the floor was far from the plane P.

Videos of this experiment are shown in Videos E-1-3-1 and E-1-3-2.

[click]
Figure E-1-3. Augmented views for different viewer's positions in Experiment 1-3. rv = rvini = 3.0.

[click]
Video E-1-3-1. Augmented views for different viewer's positions in Experiment 1-3 (1). rv = rvini = 3.0.

[click]
Video E-1-3-2. Augmented views for different viewer's positions in Experiment 1-3 (2). rv = rvini = 3.0. Upper left: Viewer background image. Upper right: Directly-observed background view. Lower left: Augmented view with projected background. Lower right: Augmented view with projected background and teapot.

Experiment 1-4: Interpolation of background parameters (1)

This experiment shows the effectiveness of the interpolation of background parameters LP, ΔθP, and ΔφP. The result of this experiment is shown in Figures E-1-4-a and E-1-4-b. The images in each figure are augmented views seen from the same twenty-five viewer's positions as those used in Experiment 1-3. Background boxes were arranged close to a vertical plane represented by the brown line in Figure E-1-0 (c), which was also used in Experiment 1-2. The boxes were given the same random rotation and displacement as those of the boxes used in Experiments 1-2 and 1-3. In the following, we mean the vertical plane for the boxes by "box plane".

The background parameter interpolation provides an appropriate boundary match between a projected background and a directly-observed background for an arbitrary viewer's position. In this experiment, the best result obtained by the interpolation is compared with the best result without the interpolation. The global parameters LPG, ΔθPG, ΔφPG are shown in Table E-1-4-1. The grid points G[i,j,k] with coordinates [ri, θj, φk] were defined by Table E-1-4-2, and the local parameters LPL, ΔθPL, ΔφPL given to the grid points are shown in Table E-1-4-3. When the interpolation is not used, only global parameters are used and local parameters are not used. In this experiment, the global parameters were selected so as to provide the best result for the viewer's initial position Qvini.

The images in Figure E-1-4-a were obtained when the interpolation was not used. The global parameters in Table E-1-4-1 make the background plane P become the same as the box plane for the viewer's initial position Qvini. Therefore, the image for Rvini = [3.0, 180, 90] in the center of Figure E-1-4-a has almost a perfect boundary match between the projected background and the directly-observed background. However, the same parameters are also used for other viewer's positions without the interpolation. Then, as the viewer goes away from Qvini, the plane P moves away from the box plane. This makes the boundary match worse. Particularly, in the images for [θv, φv] = [160, 80], [160, 100], [200, 80], and [200, 100] in the four corners of Figure E-1-4-a, there are noticeable gaps between the projected background and the directly-observed background along the cube's contour.

The images in Figure E-1-4-b were obtained when the interpolation was used. In addition to using the global parameters in Table E-1-4-1, the local parameters in Table E-1-4-3 were given to the grid points to define the linear interpolation functions FLPL, FΔθPL, and FΔφPL. The local parameters were selected so as to make the plane P become the same as the box plane for the viewer's positions at the respective grid points. In Figure E-1-4-b, the nine images with black frames were obtained directly from the local parameters given to the grid points while the other images were obtained from local parameters given by the interpolation functions. The nine images have almost perfect boundary matches between the projected background and the directly-observed background although there are some slight gaps caused by the approximation of the 3D shapes of the boxes by the plane P. The other images also have appropriate boundary matches due to the interpolation although their qualities are slightly lower than the qualities of the above nine images. The comparison between the images in Figures E-1-4-a and E-1-4-b shows that the background parameter interpolation works quite well to obtain an appropriate boundary match for an arbitrary viewer's position.

Videos of this experiment are shown in Videos E-1-4-1, E-1-4-2, and E-1-4-3.

[click]
Figure E-1-4-a. Augmented views for different viewer's positions in Experiment 1-4 (a). Background parameters are not interpolated. rv = rvini = 3.0.

[click]
Figure E-1-4-b. Augmented views for different viewer's positions in Experiment 1-4 (b). Background parameters are interpolated. rv = rvini = 3.0.

Table E-1-4-1. Global background parameters in Experiment 1-4. (a) Background parameters are not interpolated. (b) Background parameters are interpolated.
LPG ΔθPG ΔφPG
(a) 10.0 0.0 0.0
(b) 10.0 0.0 0.0

Table E-1-4-2. Definition of grid points for local background parameters in Experiment 1-4.
Minimum coordinate Maximum coordinate Number of points Interval
ri rmin = 2.5 rmax = 3.5 Nr = 3 Δr = 0.5
θj θmin = 0 θmax = 360 Nθ = 18 Δθ = 20
φk φmin = 80 φmax = 100 Nφ = 3 Δφ = 10

Table E-1-4-3. Local background parameters given to grid points in Experiment 1-4. Other grid points are given [LPL, ΔθPL, ΔφPL] = [0.0, 0.0, 0.0].
ri 3.0
θj 160 180 200
φk LPL ΔθPL ΔφPL LPL ΔθPL ΔφPL LPL ΔθPL ΔφPL
80 0.805944 20.0 -10.0 0.154266 0.0 -10.0 0.805944 -20.0 -10.0
90 0.641778 20.0 0.0 0.0 0.0 0.0 0.641778 -20.0 0.0
100 0.805944 20.0 10.0 0.154266 0.0 10.0 0.805944 -20.0 10.0

[click]
Video E-1-4-1. Augmented views for different viewer's positions in Experiment 1-4 (1). rv = rvini = 3.0. Upper: Background parameters are not interpolated. Lower: Background parameters are interpolated.

[click]
Video E-1-4-2. Augmented views for different viewer's positions in Experiment 1-4 (2). Background parameters are not interpolated. rv = rvini = 3.0. Upper left: Viewer background image. Upper right: Directly-observed background view. Lower left: Augmented view with projected background. Lower right: Augmented view with projected background and teapot.

[click]
Video E-1-4-3. Augmented views for different viewer's positions in Experiment 1-4 (3). Background parameters are interpolated. rv = rvini = 3.0. Upper left: Viewer background image. Upper right: Directly-observed background view. Lower left: Augmented view with projected background. Lower right: Augmented view with projected background and teapot.

Experiment 1-5: Interpolation of background parameters (2)

Although the result of this experiment is explained in Section 4.1 in the paper, it is also explained in this page.

The result of this experiment is shown in Figures E-1-5-a and E-1-5-b. This experiment has the same purpose as that of Experiment 1-4 and was done for a different arrangement of background boxes. The boxes were arranged close to two vertical box planes represented by the brown lines in Figure E-1-0 (e). The planes intersect perpendicularly, and the line of intersection of them is parallel to the z axis and intersects with the x axis. Both planes are 10 meters away from the origin O.

The global parameters and the local parameters are shown in Tables E-1-5-1 and E-1-5-2. The grid points were defined in the same way as Experiment 1-4 by using Table E-1-4-2.

In this experiment, the distribution of the boxes close to the two box planes needs to be approximated by a single background plane P. The images in Figure E-1-5-a were obtained when the interpolation was not used. The global parameters in Table E-1-5-1 were carefully selected such that the projected background was matched with the directly-observed background as appropriately as possible along the cube's contour for the viewer's initial position Qvini. The resulting plane P is parallel to the yz plane and 12.8 meters away from the origin O. The image for Rvini = [3.0, 180, 90] in the center of Figure E-1-5-a has an appropriate boundary match although there are some noticeable gaps caused by the approximation of the two box planes by the single plane P as well as the approximation of the 3D shapes of the boxes by the plane P. However, the other images have worse boundary matches with serious gaps due to the same parameters selected only for Qvini. The boundary matches in Figure E-1-5-a are much worse than those in Figure E-1-4-a because of the difficulty of the approximation by the single plane P.

The images in Figure E-1-5-b were obtained when the interpolation was used by the global and local parameters in Tables E-1-5-1 and E-1-5-2. The grid point with coordinates [ri, θj, φk] = [3.0, 180, 90], which are the same as Rvini, was given the same parameters in total as those given in the "without-interpolation" case, that is, LP = LPG + LPL = 12.8, ΔθP = ΔθPG + ΔθPL = 0, and ΔφP = ΔφPG + ΔφPL = 0. Consequently, the central images in Figures E-1-5-a and E-1-5-b are the same by the same plane P. The two grid points with [ri, θj, φk] = [3.0, 180, 80] and [3.0, 180, 100] were given the local parameters to make the same plane P remain. This means that the same plane P remained for a viewer's position with rv = 3.0, θv = 180, and 80 ≤ φv ≤ 100 by the interpolation. The three grid points with θj = 160 in Table E-1-5-2 were given the local parameters to make the plane P become the same as the right box plane in y ≤ 0 seen from the origin O. This is reasonable because a viewer at the position with θv = 160 sees mainly the boxes close to the right plane. In the same way, the local parameters given to the three grid points with θj = 200 make the plane P become the same as the left box plane in y ≥ 0. In Figure E-1-5-b, the nine images with black frames were obtained directly from the local parameters given to the grid points. These images have appropriate boundary matches although there are some gaps. Among them, the three images for θv = 180 have more noticeable gaps than the others have. The projected background in each of the three images has the boxes, some of which are close to the right box plane and others of which are close to the left one. The noticeable gaps were caused by the imperfectness of the approximation for the two box planes by the single plane P. The projected background in each of the remaining six images for θv = 160 and 200 has the boxes, all of which are close to only one of the two box planes. The single plane P works quite well to approximate the distribution of the boxes. On the other hand, the images other than the above nine images were obtained from local parameters given by the interpolation functions. These images also have appropriate boundary matches due to the interpolation although there are also some gaps. Among them, the two images for θv = 180 have some noticeable gaps and the four images for θv = 160 and 200 have less gaps by the same reason as that for the images with black frames. The ten images for θv = 170 and 190 have noticeable gaps although the projected background in each image has the boxes, all of which are close to only one of the two box planes; this situation of the boxes is the same as that for θv = 160 and 200. The background parameters for θv = 170 are obtained by interpolating the parameters given to the grid points for θv = θj = 160 and 180. This means that the background plane P170 is the intermediate between the two planes P160 and P180, where Pθv means a plane for θv. Thus, the noticeable gaps for θv = 170 were caused by the plane P170 that did not coincide with the box plane. The same applies to the case of θv = 190. Compared to Figure E-1-5-a, the boundary matches were greatly improved in Figure E-1-5-b by the background parameter interpolation although there were some gaps, part of which were noticeable.

The result of this experiment shows that the background parameter interpolation has the fundamental ability to make the boundary match between a projected background and a directly-observed background as appropriate as possible for an arbitrary viewer's position. This ability achieves the effective view-dependent projection to make the viewer not feel the presence of a real object but feel a virtual object merging into the real world.

Videos of this experiment are shown in Videos E-1-5-1, E-1-5-2, and E-1-5-3.

[click]
Figure E-1-5-a. Augmented views for different viewer's positions in Experiment 1-5 (a). Background parameters are not interpolated. rv = rvini = 3.0.

[click]
Figure E-1-5-b. Augmented views for different viewer's positions in Experiment 1-5 (b). Background parameters are interpolated. rv = rvini = 3.0.

Table E-1-5-1. Global background parameters in Experiment 1-5. (a) Background parameters are not interpolated. (b) Background parameters are interpolated.
LPG ΔθPG ΔφPG
(a) 12.8 0.0 0.0
(b) 10.0 0.0 0.0

Table E-1-5-2. Local background parameters given to grid points in Experiment 1-5. Other grid points are given [LPL, ΔθPL, ΔφPL] = [0.0, 0.0, 0.0].
ri 3.0
θj 160 180 200
φk LPL ΔθPL ΔφPL LPL ΔθPL ΔφPL LPL ΔθPL ΔφPL
80 1.203993 -25.0 -10.0 2.997460 0.0 -10.0 1.203993 25.0 -10.0
90 1.033779 -25.0 0.0 2.8 0.0 0.0 1.033779 25.0 0.0
100 1.203993 -25.0 10.0 2.997460 0.0 10.0 1.203993 25.0 10.0

[click]
Video E-1-5-1. Augmented views for different viewer's positions in Experiment 1-5 (1). rv = rvini = 3.0. Upper: Background parameters are not interpolated. Lower: Background parameters are interpolated.

[click]
Video E-1-5-2. Augmented views for different viewer's positions in Experiment 1-5 (2). Background parameters are not interpolated. rv = rvini = 3.0. Upper left: Viewer background image. Upper right: Directly-observed background view. Lower left: Augmented view with projected background. Lower right: Augmented view with projected background and teapot.

[click]
Video E-1-5-3. Augmented views for different viewer's positions in Experiment 1-5 (3). Background parameters are interpolated. rv = rvini = 3.0. Upper left: Viewer background image. Upper right: Directly-observed background view. Lower left: Augmented view with projected background. Lower right: Augmented view with projected background and teapot.

E-2. Experiment in real environment

We secondly made experiments in real environments to evaluate the practical performance of our method. The following three experiments are described in Section 4.2 in the paper. Therefore, we only show their videos and do not explain their details in this page; some frame images of the videos are shown in Figures 7, 8, and 9 in the paper.

The devices used in the experiments are shown in Table E-2-0. A white cube made from styrofoam was used as a real object; its size was 0.4 × 0.4 × 0.4 meters. The 3D geometric model used as a virtual object is shown in Video E-2-0. Viewer virtual object images were obtained by rendering the model in advance for Mr × Mθ × Mφ = 1 × 360 × 1 discrete viewer's positions, that is, for every one degree around the model.

Table E-2-0. Devices used in experiments in real environments.
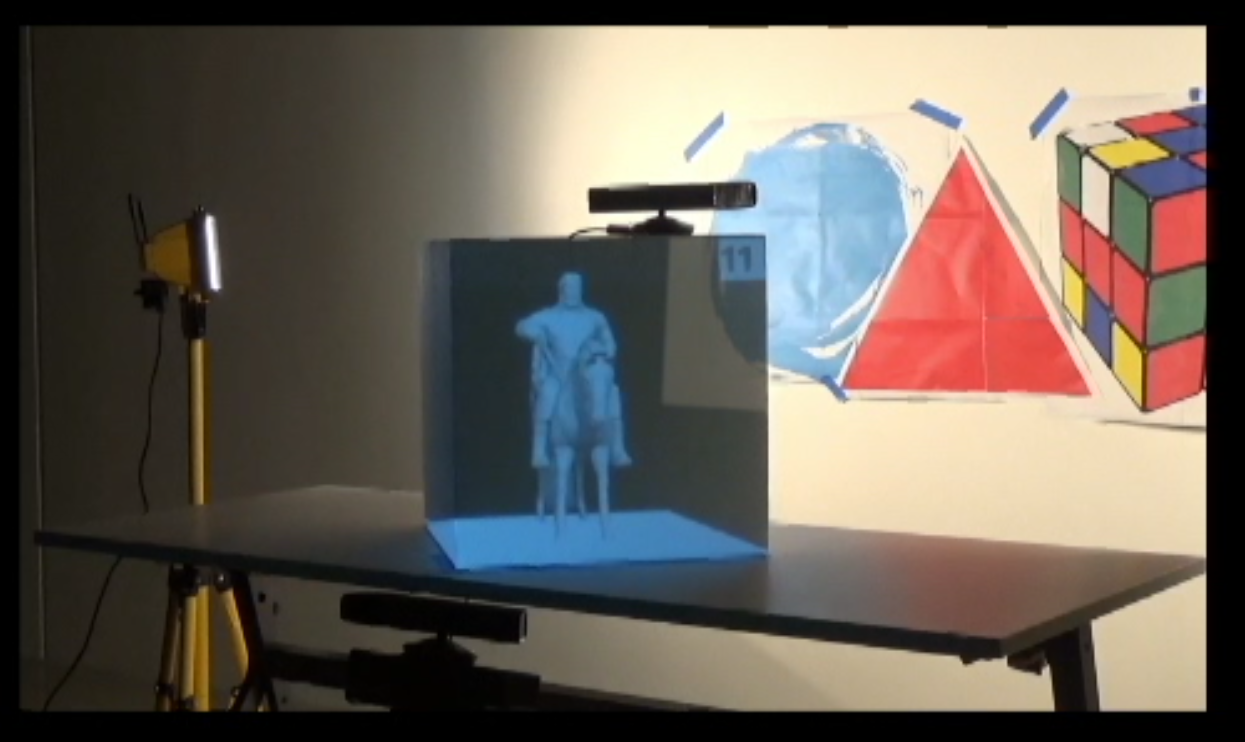
Projector RICOH IPSiO PJ WX5150
Tracking sensor Kinect for Windows
Camera Kinect for Windows
Personal computer OS: Windows 10, Chipset: Intel(R) Z370 Express, CPU: Intel(R) Core i7-8700K (3.7-4.7GHz), GPU: NVIDIA(R) GeForce GTX 1060 6GB GDDR5, Mem: 32GB, SSD: 480GB, HDD: 2TB.

[click]
Video E-2-0. Virtual object used in experiments in real environments.

Experiment 2-1: Near planar background

The background was a planar wall with three figures near the cube.

[click]
Video 2-1. Augmented view for near planar background in Experiment 2-1.

Experiment 2-2: Near non-planar background

The background had a rack containing some boxes in front of the wall used in Experiment 2-1.

[click]
Video 2-2. Augmented view for near non-planar background in Experiment 2-2.

Experiment 2-3: Far complicated-shaped background

The background was far from the cube and the background objects had complicated shapes. The black jaggy-shaped wall was about 10 meters and the white wall behind it was about 15 meters away from the cube. There were many background objects in front of the walls, such as desks and chairs.

[click]
Video 2-3. Augmented view for far complicated-shaped background in Experiment 2-3.